前回に引き続き、マルコフ決定問題を解いていきます。
前回は状態遷移確率がわかっているものであるとして計算をしていましたが、現実は必ずしも遷移確率がわかるとは限りません。
そのような場合に、前回の評価関数 \(Q_{t}(i, k)\) の漸化式を少し変え、確率の推定を行わずにその場のノリで \(Q_t\) を更新していく方法が取られることがあります。
このような学習方法を直接法といいます。
Q-learningも直接法の一つで、この方法では以下のように変更された漸化式で \(Q\) の近似値を求めていきます。
\[ Q_{t+1}(i, k) = (1 - \alpha_{t}(i, k))Q_{t}(i, k) + \alpha_{t}(i, k)(c_{ijk} + \gamma \min_{k’}\{ Q_t(j, k’) \}) \]
ただし、上式での \(j\) は実際に状態 \(i\) で行動 \(k\) を取った時に遷移した先の状態を表します。
また、 \(0 \leq \alpha_t(i, k) < 1\) は学習率という関数です。この値を調節することで、直前の経験をどれだけ以降の行動の決定に反映させるかが決まります。この学習率が \(\frac{1}{t}\) 程度のオーダーのとき、 \(Q_t\) は実際の値に収束することが知られています。
このQ-learningを実際に動かせるデモを作ってみました。
以下がデモページになります。
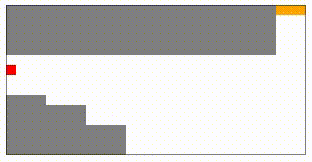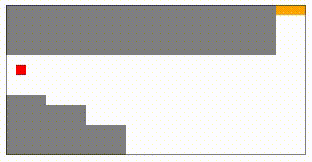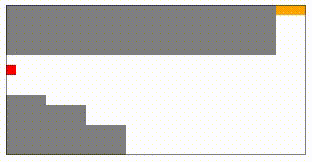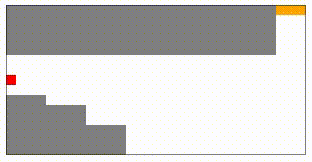
開いてみると、こんな感じの図が出て来るはずです。

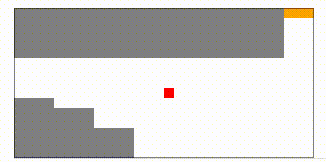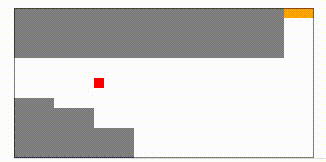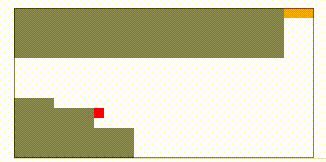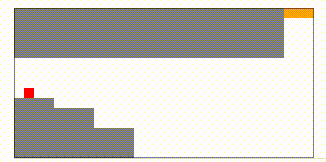
図のグレーの部分は壁で、赤い部分が車、オレンジがゴールを表しています。
この車はQ-learningで学習を行い、徐々にゴールに辿り着く確率が上がってきます。
最初は上の図のようにスタート地点の付近を少し動いてはスタートに戻り…という動作を繰り返していますが、100000ラウンドほど学習させてみると…
このように、ある程度遠くまで動くことができるようになっているのがわかります。
さらに1000000ラウンドほど学習させてみると、
このように、難なくゴールに辿り着くことができるようになっています。