タイトルは釣りです。
FXに関しては全くの初心者ですが、適当に分析してみたらなんとなくそれっぽい結果が出てきたので紹介したいと思います。
機械学習の勉強のついでにFXの価格予測でもやって一儲けできたら一石二鳥だなーと思い、一番簡単な分類方法として、ドル円が値上がりするかどうかが線形分離できないか試してみました。
今回は線形分離用のアルゴリズムの中でも最も簡単な部類に入る、パーセプトロンを使って分類を行います。
実際に分類を行ってみたところ、そこそこの適合率でドル円の値上がりを予測することができるようになりました。
なお、以下ではライブラリとしてbatteries, lwt, cohttp, yojson, gnuplotが#requireされていることが前提となっています。
銘柄のデータの取得
ドル円の価格は、OANDAのAPIを使って取得しました。
(* oanda_show_candles.ml *)
open Lwt
open Cohttp
open Cohttp_lwt_unix
let api_token = "MY_TOKEN"
let base_url = "https://api-fxpractice.oanda.com/v1"
let rec write_to_stdout (body : string Lwt_stream.t) : unit Lwt.t =
Lwt_stream.get body >>= fun stropt ->
match stropt with
| None -> return ()
| Some str ->
Lwt_io.write Lwt_io.stdout str >>= fun () ->
write_to_stdout body
let candles (instrument : string) : unit Lwt.t =
Client.get (Uri.add_query_params (Uri.of_string (base_url ^ "/candles"))
[("instrument", [instrument]);
("count", ["5000"]);
("granularity", ["H1"])
])
~headers:(Header.of_list [("Authorization", "Bearer " ^ api_token);
("X-Accept-Datetime-Format", "UNIX");
("Content-Type", "x-www-form-urlencoded");
("Accept-Encoding", "gzip, deflate")])
>>= fun (resp, body) ->
let status = Response.status resp in
if (Code.code_of_status status) <> 200
then Cohttp_lwt_body.to_string body >>= fun (b) ->
fail_with (Code.string_of_status status ^ "\n" ^ b)
else write_to_stdout (Cohttp_lwt_body.to_stream body)
let () =
catch (fun () -> candles "USD_JPY")
(function
| Failure msg -> print_endline msg; return ()
| _ -> print_endline "unknown error"; return ())
|> Lwt_main.run
これを実行すると、直近5000件分の一時間足のドル円のデータが手に入ります。
$ ocamlfind ocamlopt -o oanda_show_candles.native -linkpkg -package cohttp,lwt,cohttp.lwt,yojson oanda_show_candles.ml
$ ./oanda_show_candles.native > candles.json
得られたデータは以下のような書式になっています。
$ head -n17 candles.json
{
"instrument" : "USD_JPY",
"granularity" : "H1",
"candles" : [
{
"time" : "1474311600000000",
"openBid" : 101.804,
"openAsk" : 101.819,
"highBid" : 101.842,
"highAsk" : 101.858,
"lowBid" : 101.772,
"lowAsk" : 101.786,
"closeBid" : 101.831,
"closeAsk" : 101.847,
"volume" : 567,
"complete" : true
},
実際にどのようなデータが取得できたか見てみましょう。以下のようなコードを書いて、グラフを表示してみました。
(* oanda_candle_chart.ml *)
open Yojson.Basic.Util
open Gnuplot
type json = Yojson.Basic.json
let candles : json list =
let json = Yojson.Basic.from_file "candles.json" in
json |> member "candles" |> to_list
let avg_bid_of_candle (candle : json) : float =
let highBid = candle |> member "highBid" |> to_number in
let lowBid = candle |> member "lowBid" |> to_number in
(highBid +. lowBid) /. 2.
let avg_ask_of_candle (candle : json) : float =
let highAsk = candle |> member "highAsk" |> to_number in
let lowAsk = candle |> member "lowAsk" |> to_number in
(highAsk +. lowAsk) /. 2.
let time_of_candle (candle : json) : float =
candle |> member "time" |> to_string |> float_of_string
let () =
let bid_xys = BatList.map (fun c -> (time_of_candle c, avg_bid_of_candle c)) candles in
let ask_xys = BatList.map (fun c -> (time_of_candle c, avg_ask_of_candle c)) candles in
let gp = Gp.create () in
Gp.plot_many gp
[ Series.lines_xy bid_xys ~title:"Bid" ~color:`Blue
; Series.lines_xy ask_xys ~title:"Ask" ~color:`Red ];
Gp.close gp
実行すると、一時間ごとのBidとAskの平均値(のようなもの)が表示されます。なお、横軸はunix timeを表しています。
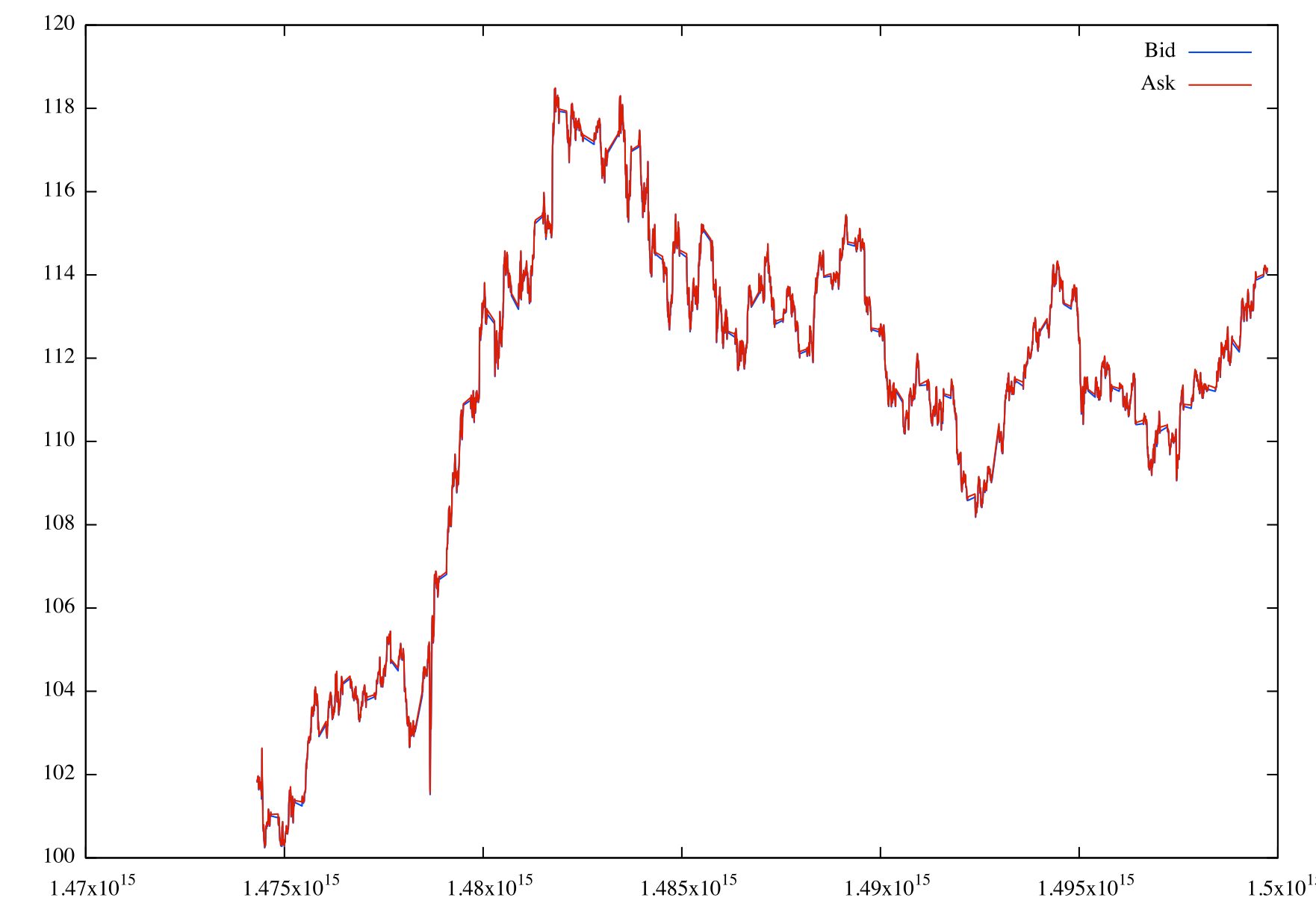
分類する
手に入れたデータを使って、実際に分類を行ってみます。
今回は、その時間の平均的な価格でドル円を買い、一時間後に適当なタイミングで売った場合に、利益が出るタイミングがあるかどうかが、その時間のopenBid, openAsk, highBid, highAsk, lowBid, lowAsk, closeBid, closeAskの重み付き和で予測できると仮定し、実際にそのような分類を行うことのできる分類器を求めてみました。
今回はただの練習なので、線形分類器の実装は最も単純なものの一つであるパーセプトロンをつかってみました。
パーセプトロンはこの前作ったやつと同じものを使用します。
module P = Perceptron (struct
let dim = 8
let eta = 1.
end)
観測データとしては、後から説明する理由により、取得した5000件のデータのうち、最後のものを除いた4999件を利用します。
open Yojson.Basic.Util
type json = Yojson.Basic.json
let candle_to_point (candle : json) : vec =
Vec.of_list [
candle |> member "openBid" |> to_number;
candle |> member "openAsk" |> to_number;
candle |> member "highBid" |> to_number;
candle |> member "highAsk" |> to_number;
candle |> member "lowBid" |> to_number;
candle |> member "lowAsk" |> to_number;
candle |> member "closeBid" |> to_number;
candle |> member "closeAsk" |> to_number
]
let candles =
let json = Yojson.Basic.from_file "candles.json" in
json |> member "candles" |> to_list
(* candlesのうち、最後の1つを除いたものを、パーセプトロンで分類できるベクトルにしたもの *)
let points = BatList.map candle_to_point (candles |> BatList.rev |> BatList.tl |> BatList.rev)
利益が出るかどうかの判断の仕方については、以下のように考えます。
あるタイミングで買って、その一時間後のあるタイミングで売るとします。このとき、手数料などを考慮しなければ、
現在のAsk < 一時間後のあるタイミングでのBid
となっていれば利益が出せると言えます。
ここで、現在のAskについては、その時間の平均的な値として、(highAsk + lowAsk) / 2を使うことにします。
また、一時間後のBidについて、あるタイミングで一瞬でも買値を上回っていれば利益は出せると考えて、highBidを使うことにします。
以上の計算結果により利益が出せると判断されれば1, そうでなければ-1でデータをラベル付けして、二値分類を行っていきます。
なお、各時間のデータについて、その一時間後のデータも無ければラベルが求まらないため、先ほど取得した5000件のデータのうち、最後のものを除いた4999件のデータを使用することにします。
let categories_of_candles (candles : json list) : float list =
let diff candle next =
let lowAsk1 = candle |> member "lowAsk" |> to_number in
let highAsk1 = candle |> member "highAsk" |> to_number in
let highBid2 = next |> member "highBid" |> to_number in
if (highBid2 -. (lowAsk1 +. highAsk1) /. 2.) > 0. then 1. else -1. in
BatList.map2 diff
(candles |> BatList.rev |> BatList.tl |> BatList.rev)
(BatList.tl candles)
let categories = categories_of_candles candles
このうち、過去の4000件を学習データとし、残りの999件をテストデータとしました。
let training_points, production_points = BatList.split_at 4000 points
let training_categories, production_categories = BatList.split_at 4000 categories
あとは、この前作ったパーセプトロンを使って分類するだけです。
まずは、分類器wを作ります。
let w = P.initial_hyp ()
そしてエポックを定義し、適当に回していきます。
let epoch (h : P.hyp) (ps : vec list) (cs : float list) : int * int =
let round (ok, ng) point category =
let category' = P.evaluate h point in
P.round h point category;
if category *. category' <= 0.
then (ok, ng + 1)
else (ok + 1, ng) in
BatList.fold_left2 round (0, 0) ps cs
# let _ = epoch w training_points training_categories;;
- : int * int = (2758, 1242)
例によって、epochの戻り値は(分類に成功した数, 分類に失敗した数)となっています。
現段階では4000個のデータのうち、2758個の分類に成功しているようです。
毎回手打ちでエポックを回すのは大変なので、以下のような関数を定義し連続でエポックを回していきます。
let rec times n action res =
if n < 0 then failwith "n < 0!"
else if n = 0 then res
else let res' = action () in times (n - 1) action res'
# let _ = times 10000 (fun () -> epoch w training_points training_categories) (0, 0);;
- : int * int = (2863, 1137)
# let _ = times 10000 (fun () -> epoch w training_points training_categories) (0, 0);;
- : int * int = (2954, 1046)
全部で20001エポック回したことになりました。
この時点で訓練データのうち分類に成功しているものの数は2954個です。
2954 / 4000 = 0.7385なので、訓練データについては74%くらい正しく分類できてることがわかります。
結果
分類器の適合率を求めてみます。
今回の場合、適合率は以下のような式で表されます。
分類器が値上がりすると判断したもののうち、実際に値上がりしたものの数
適合率 = ----------------------------------------------------------------------
分類器が値上がりすると判断したものの数
これを実際に、テストデータについて計算してみます。
let precision =
let (n, m) = BatList.fold_left2
(fun (n, m) candle cat ->
let cat' = P.evaluate w candle in
if cat > 0. && cat' > 0. then (n + 1, m + 1)
else if cat' > 0. then (n, m + 1)
else (n, m))
(0, 0) test_points test_categories in
float_of_int n /. float_of_int m
この値を見てみると、
# precision;;
- : float = 0.877344877344877316
適合率は約88%であることがわかりました。それなりに高いですね。
# BatList.fold_left (fun n x -> if P.evaluate w x > 0. then (n + 1) else n) 0 test_points;;
- : int = 693
上のコードにより、テストデータ999件のうち、分類器が値上がりすると判断した回数は693回であることがわかります。
ということは、テストデータの中で分類器が値上がりすると判断したもののうち、実際に値上がりしたものの個数は693 * precision = 608個となり、そうでなかったものの個数は693 * (1 - precision) = 85回となります。
したがって、もしこの分類器が値上がりすると判断した時にドル円を買って、一時間後の適当なタイミングで売ったとすると、608回は利益が出て、85回は損失が発生する計算になります。
テストデータ999件は約41日分なので、取引間の値幅の平均をCとすると、この分類器を使えば、テストデータの約41日間で(608 - 85)C = 523C円儲けたことになります。Cは1回の取引額に比例して大きくなっていくので、それなりの額をつぎ込めば利益もそれなりの量になるのではないでしょうか?
単純な線形分類器を使っただけでも、これくらい面白い結果が出てくるということがわかりました。
オチ
一見今回の方法はうまくいってそうですが、現実に使うためには以下のような問題があります。
今回の分析では、ある瞬間においてその瞬間を含む一時間足のhighBidやcloseBidなどがわかることが前提となっていました。しかし、現実にはそのような状況はありえません。
また、今回は手数料などを考慮しておらず、また実際にどの程度値上がりするかも考慮されていないため、本当に儲かるかどうかに関しては疑問が残ります。