高速にアクセスができ、かつ理論上最も効率よくデータを圧縮した場合と同程度に小さなデータ構造のことを簡潔データ構造といいます。
今回は簡潔データ構造のうち、最も基本的なものの一つであるBit Vectorについて紹介したいと思います。
Bit Vector
Bit Vectorは文字通り1ビットの値の列で、通常は以下の2種類の操作について考えます。
- \( rank(B, x) \) : Bit Vector B の第 0..x 番目までの要素のうち、1の数
- \( select(B, x) \) : Bit Vector B の先頭から x 番目の 1 の位置
今回は、この2つの操作のうち \( rank(B, x) \) についてのみ説明します。

上の図のように \( B_n \) の要素が並んでいるとして、最も簡単で高速な \( rank \) の求め方は、事前にすべての \( rank \) の値を計算しておき、その値を保存しておくことです。
この時の計算量は \( O(1) \) となり、メモのサイズは \( n\log n \) ビットとなります。
Rankの改良
rankの計算速度を早くする方法として、途中までの計算をメモしておくことにします。
以下のようにB全体を長さ \( \log^2n \) のブロックに分けます。
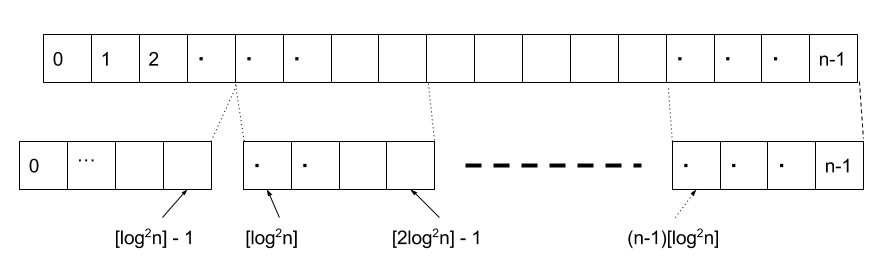
そして長さ \( \lfloor \frac{n}{\log^2n} \rfloor \) の配列 \( R_i \) を作り、 \( i \) 番目に \( B_{0}..B_{\lfloor \frac{n}{\log^2n} \rfloor - 1} \) の \( rank \) を保存しておきます。
そうすることによって、\( rank(B, x) \) を求めるときに、以下の赤枠で囲った部分はすべて計算済みになるため、x自身の属するブロックのみを調べれば \( rank \) が求まることになります。
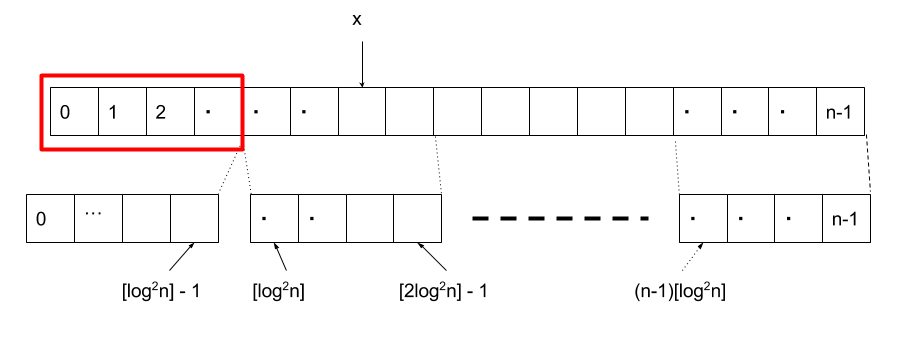
したがって、計算量は \( O(\log^2 n) \) となり、配列 \( R_i \) のサイズは、各要素が \( \log n \) ビットあれば充分なので、
\[ \frac{n}{\log^2 n} \times \log n = \frac{n}{\log n} \mathrm{bits} \]
となります。
さらに改良
先ほどのブロックをさらに長さ \( \frac{1}{2}\log n \) の小さなブロックに分割します。(以後、このブロックを小ブロックと呼び、前のフェースで分割されたブロックを大ブロックと呼びます。)
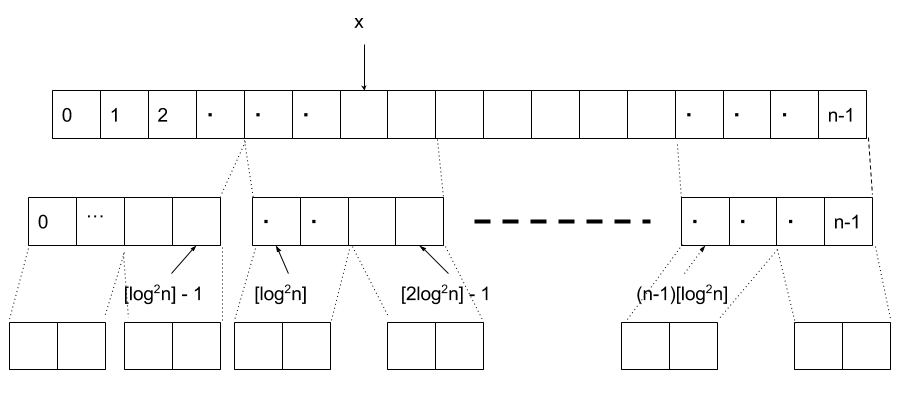
そして、大ブロックの先頭からそれに属する小ブロックの最後の要素の \( rank \) を新しい配列 \( S_i \) に保存すれば、更に高速に \( rank \) を求めることができるようになります。
例えば、先ほどの例で言えば図の赤枠部分と青枠部分はすでに求まっているため、あとはx自身が属する小ブロックのみを調べることによって、 \( rank \) が求まることになります。
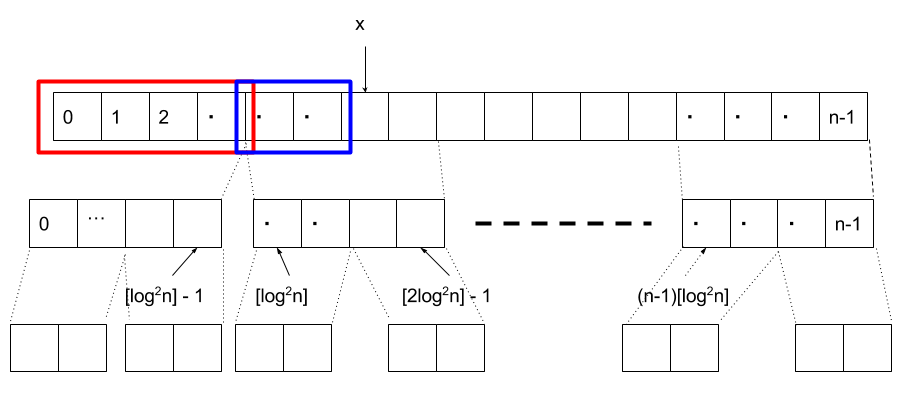
したがって、計算量は \(O(\frac{1}{2}\log n) = O(\log n) \) となり、配列 \( S_i \) のサイズは、各要素が \( \log (\log^2 n) \) ビットあれば充分なので、
\[ \frac{n}{\frac{1}{2}\log n} \times \log(\log^2 n) = \frac{4 n \log \log n}{\log n} \mathrm{bits} \]
となります。
もっと改良
最後に、残った小ブロック内のrankを高速化します。小ブロックは長さ \( \frac{1}{2}\log n \) のビット列なので、その種類は \(2^{\frac{1}{2}\log n} = \sqrt{n} \) 種類となります。
さらに、そのうちxの小ブロック内での位置は \( \frac{1}{2}\log n \) 通りなので、\( \sqrt{n} \times \frac{1}{2}\log n \) のテーブルを作り、小ブロックの中身とxの位置としてあり得る組み合わせをすべてメモしておきます。
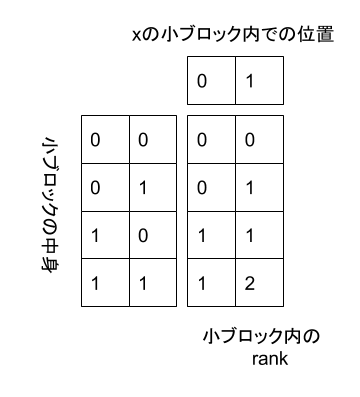
こうすることによって、残った小ブロック内のrankも定数時間で求める事ができるようになります。
また、このテーブルのサイズは、各要素が \( \log(\frac{1}{2}\log n) \) ビットあれば充分なので、
\[ \frac{\sqrt{n}\log n}{2} \times \log(\frac{1}{2}\log n) \]
\[ = O(\sqrt{n}\log n \log \log n) \]
\[ = o(\frac{n \log \log n}{\log n}) \mathrm{bits} \]
となります。
まとめ
以上により、 \( rank(B, x) \) を求めるには3種類の配列の要素を持ってきて足し合わせるだけで済むようになるので、定数時間で計算できることがわかりました。
さらに、このときのデータ構造のサイズは \( n + o(\frac{n \log \log n}{\log n}) \) ビットとなり、一番最初の方法よりかなりメモリ使用量を抑えることができます。